Что такое параллелепипед: определение, элементы, виды, свойства
В данной публикации мы рассмотрим определение, элементы, виды и основные свойства параллелепипеда, в т.ч. прямоугольного. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение параллелепипеда
Параллелепипед – это геометрическая фигура в пространстве; шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.
Параллелепипед – это разновидность призмы с параллелограммом в качестве оснований. Основные элементы фигуры те же, что и у призмы.
Примечание: Формулы для расчета площади поверхности (для прямоугольной фигуры) и объема параллелепипеда представлены в отдельных публикациях.
Виды параллелепипедов
Свойства параллелепипеда
1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами.
2. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам.
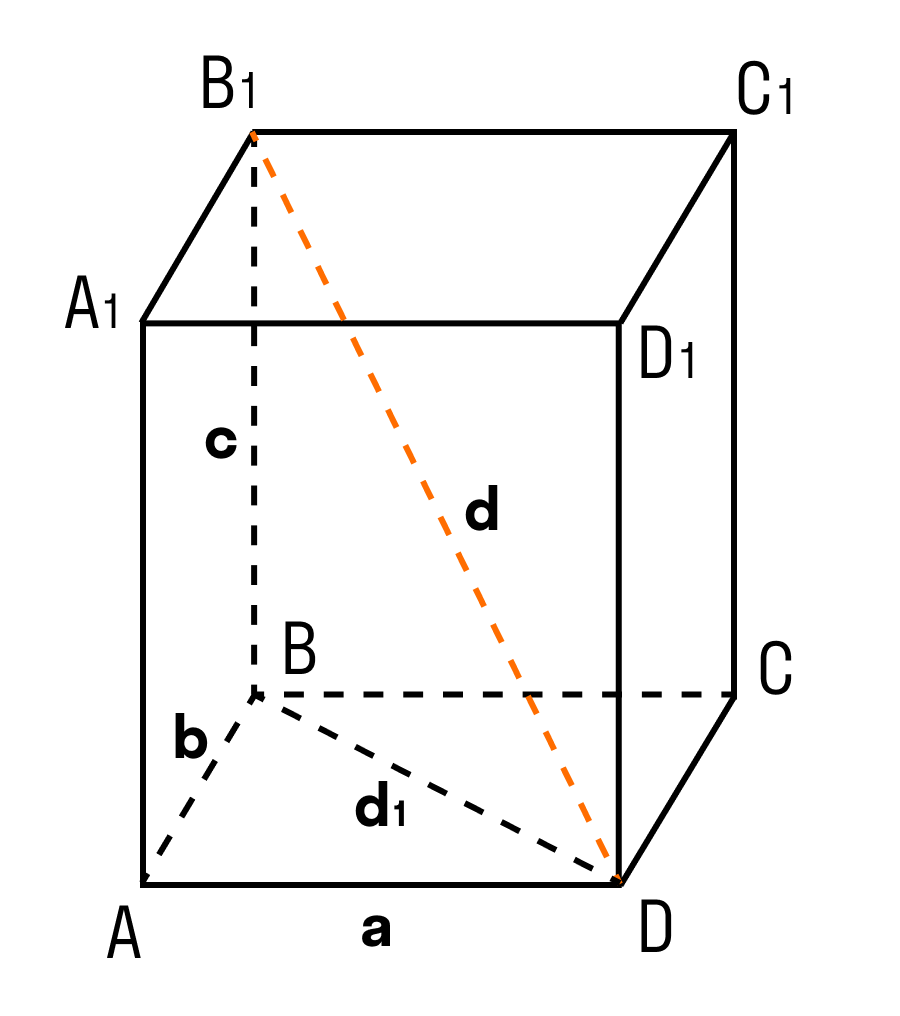
3. Квадрат диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины (a), ширины (b) и высоты (c).
d 2 = a 2 + b 2 + c 2
Примечание: к параллелепипеду, также, применимы свойства призмы.
Параллелепипед (ЕГЭ 2022)
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Читай статью, смотри вебинар и ты все про него будешь знать!
Параллелепипед — коротко о главном
Параллелепипед — это четырехугольная призма (многогранник с \( \displaystyle 6\) гранями), все грани которой — параллелограммы.
Прямой параллелепипед —это параллелепипед, у которого \( \displaystyle 4\) боковые грани — прямоугольники.
Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники
Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства параллелепипеда
Параллелепипед — подробнее
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.
Далее смотри на картинки, запоминай и не путай!
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
Свойства параллелепипеда
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.
Прямой параллелепипед
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольный параллелепипед
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.
Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.\( \displaystyle <
^<2>>=<^<2>>+<^<2>>+< ^<2>>\).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Прямоугольный параллелепипед. Что это такое?
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
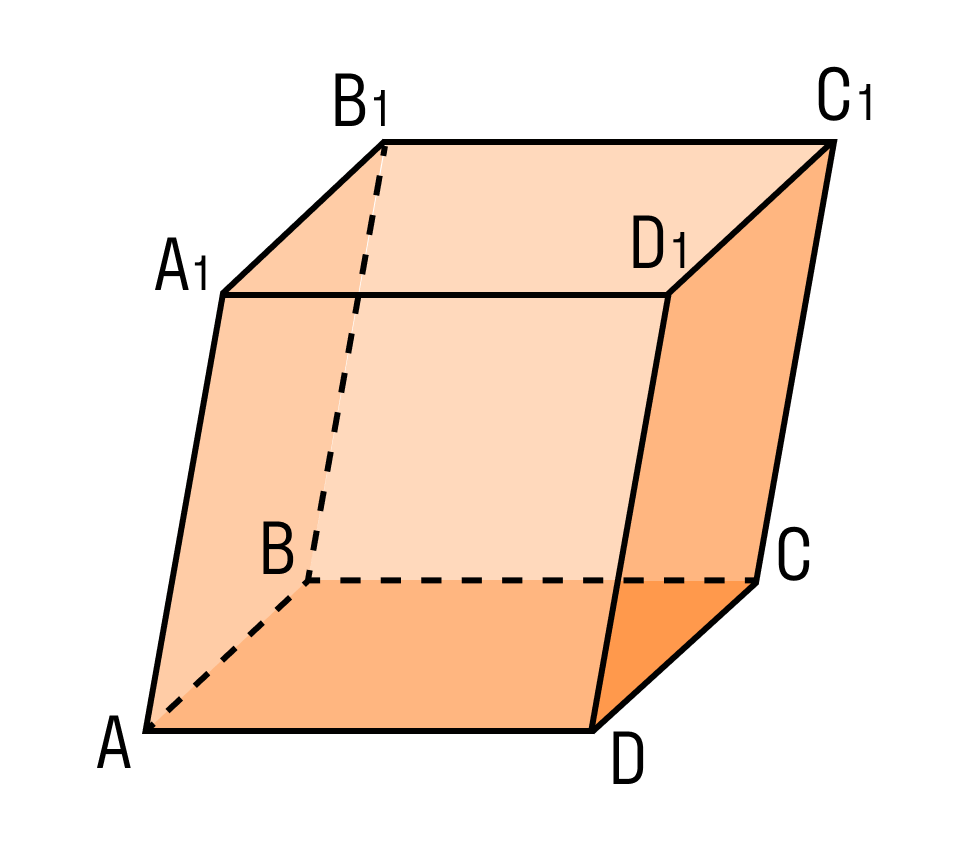
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
Формулы прямоугольного параллелепипеда:
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
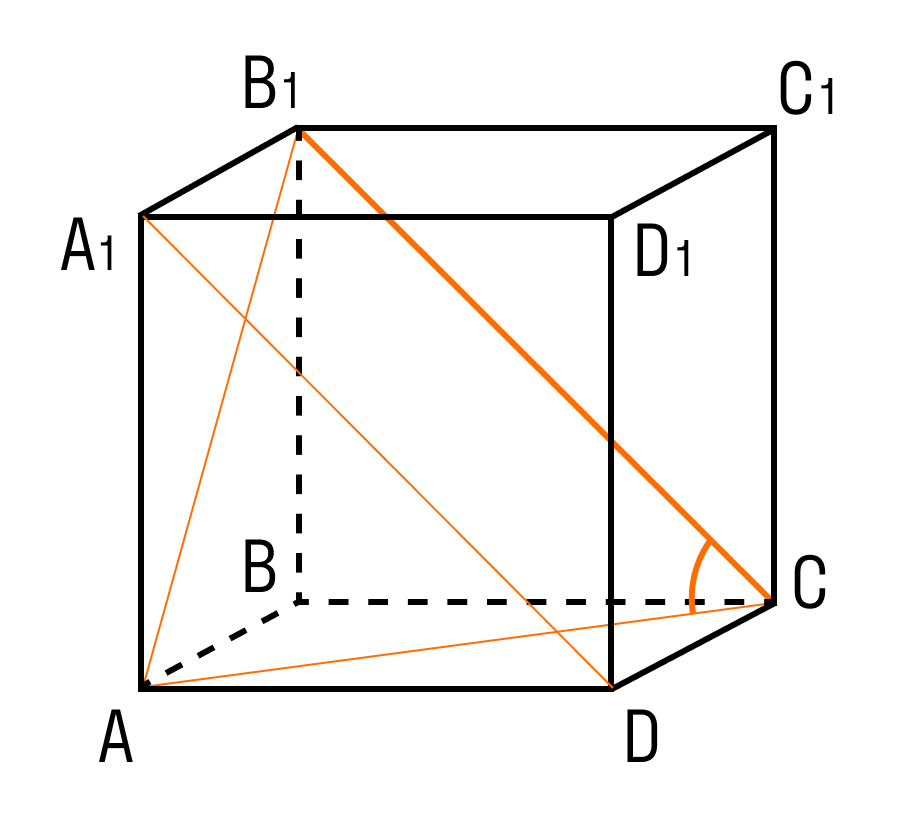
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
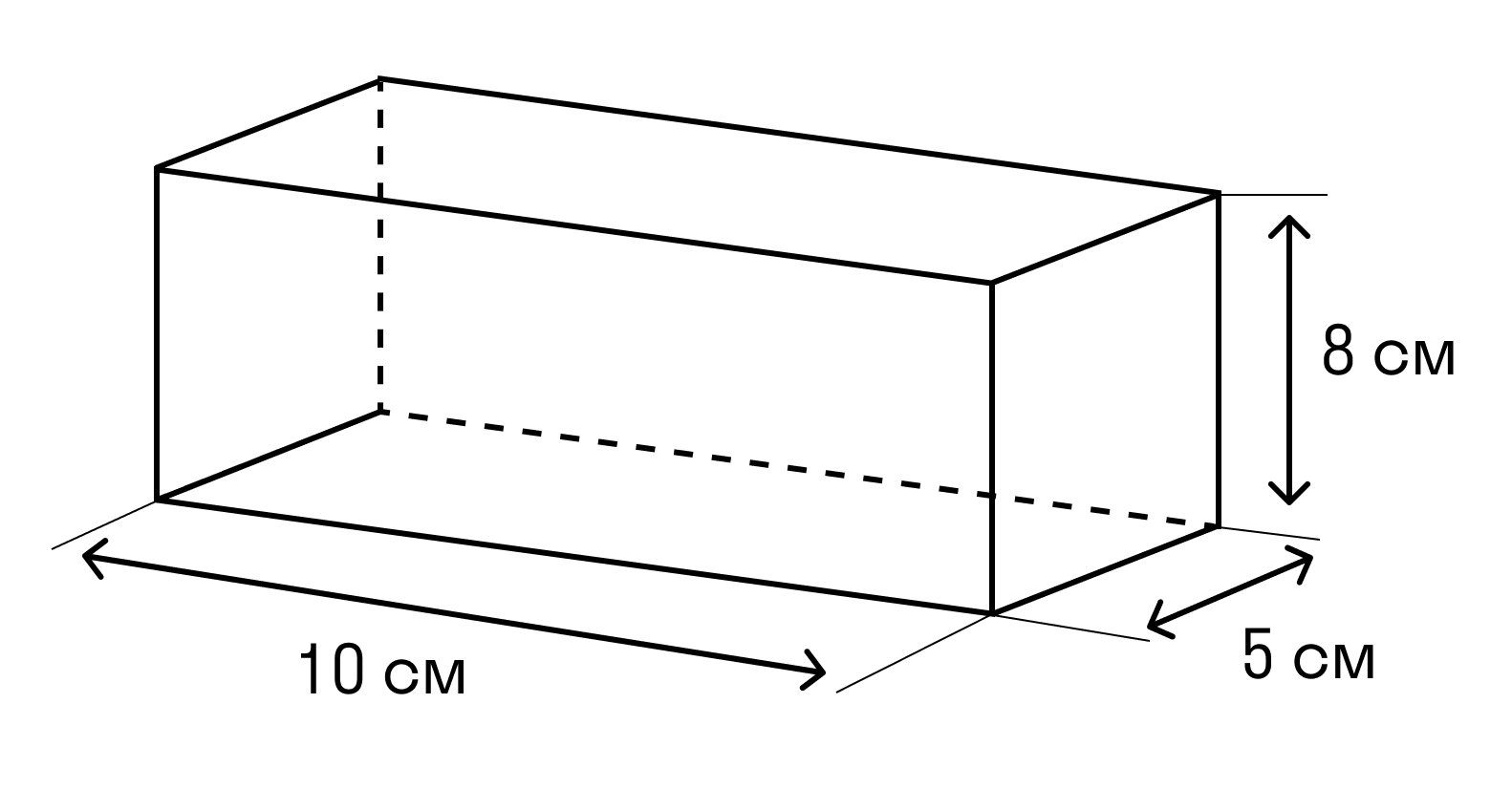
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
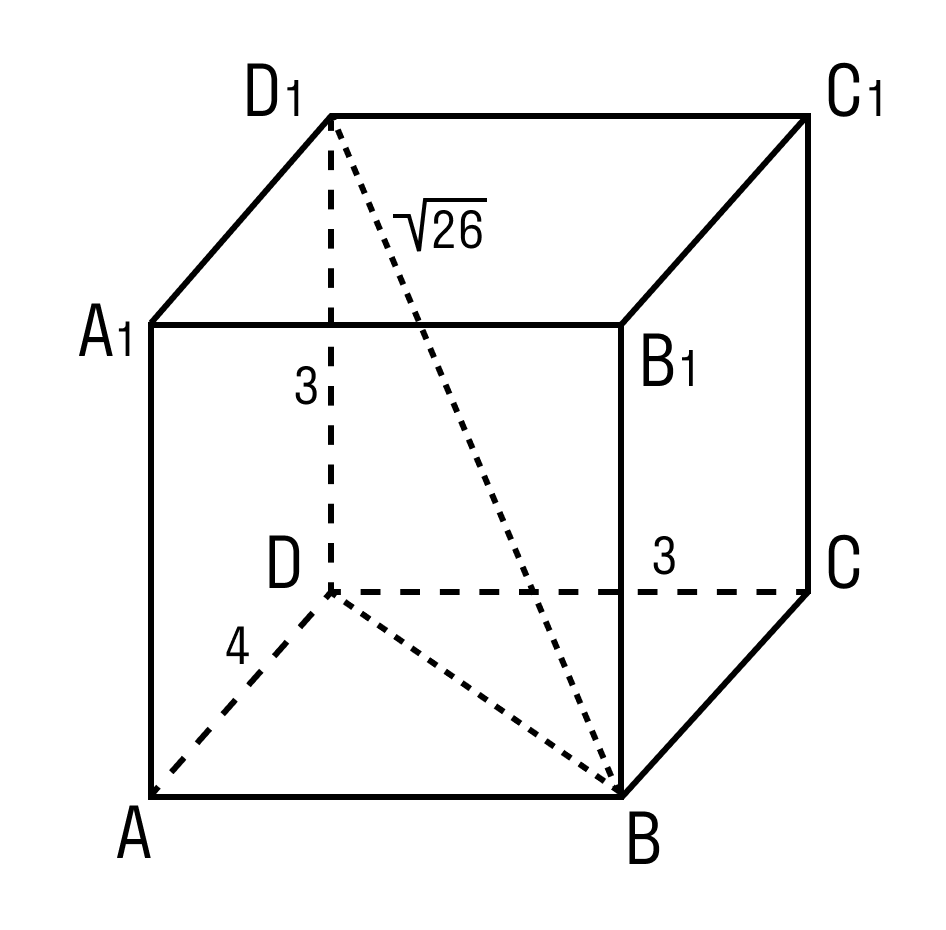
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.
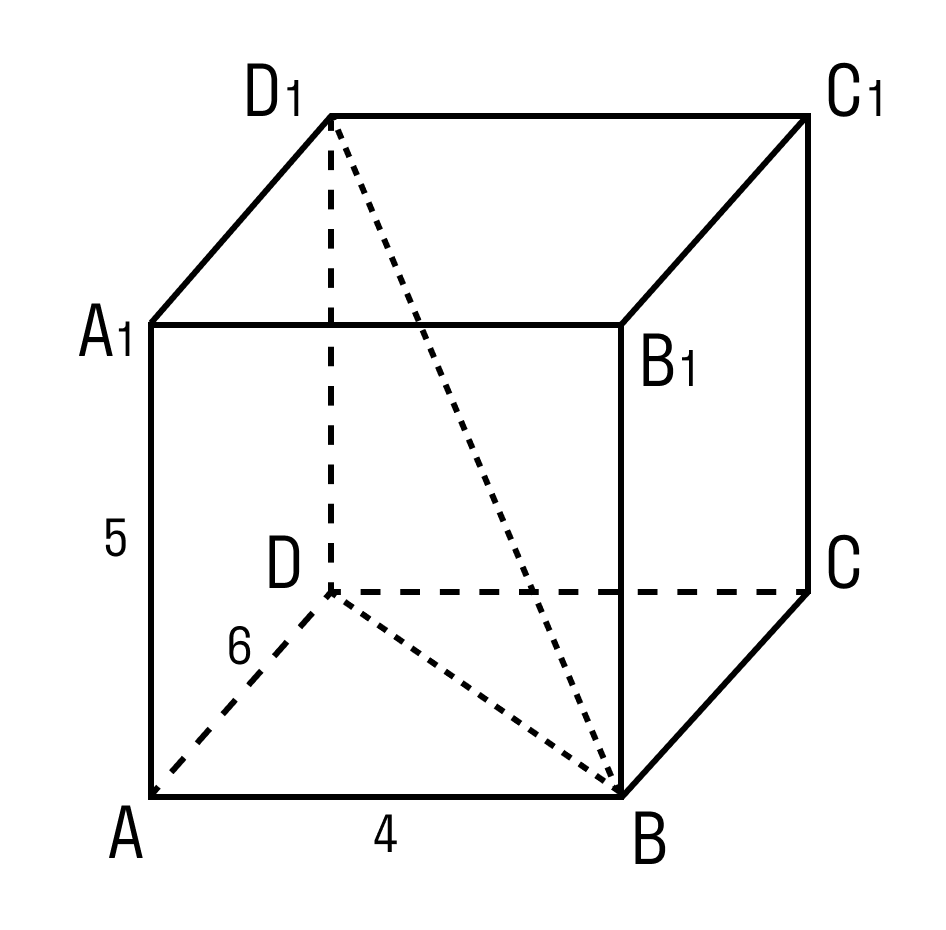
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
Геометрические фигуры. Параллелепипед.
Параллелепипед — призма, основанием которой является параллелограмм либо (равносильно) многогранник с шестью гранями, являющимися параллелограммами. Шестигранник.
Параллелограммы, из которых состоит параллелепипед являются гранями этого параллелепипеда, стороны этих параллелограммов являются ребрами параллелепипеда, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда каждая грань является параллелограммом.
Как правило выделяют любые 2-е противолежащие грани и называют их основаниями параллелепипеда, а оставшиеся грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям являются боковыми ребрами.
2 грани параллелепипеда, которые имеют общее ребро являются смежными, а те, которые не имеют общих ребер — противоположными.
Отрезок, который соединяет 2 вершины, которые не принадлежат 1-ой грани является диагональю параллелепипеда.
Длины ребер прямоугольного параллелепипеда, которые не параллельны, являются линейными размерами (измерениями) параллелепипеда. У прямоугольного параллелепипеда 3 линейных размера.
Типы параллелепипеда.
Существует несколько видов параллелепипедов:
Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.
Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.
Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов.
Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты.
Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.
Свойства параллелепипеда.
В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.
Определения параллелепипеда. Основные свойства и формулы
Параллелепипед – это геометрическая фигура, все 6 граней которой представляют собой параллелограммы.
В зависимости от вида этих параллелограммов различают следующие виды параллелепипеда:
Прямым параллелепипедом называют четырехугольную призму, ребра которой составляют с плоскостью основания угол 90 °.
Прямоугольным параллелепипедом называют четырехугольную призму, все грани которой являются прямоугольниками. Куб есть разновидность четырехугольной призмы, у которой все грани и ребра равны между собой.
Свойства параллелепипеда
Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:
Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.
Формулы параллелепипеда
Для поиска ответов на поставленную задачу недостаточно знать только свойства фигуры. Также могут понадобиться и некоторые формулы для нахождения площади и объема геометрического тела.
Площадь оснований находится также как и соответствующий показатель параллелограмма или прямоугольника. Выбирать основание параллелограмма можно самостоятельно. Как правило, при решении задач проще работать с призмой, в основании которой лежит прямоугольник.
Формула нахождения боковой поверхности параллелепипеда, также может понадобиться в тестовых заданиях.
Примеры решения типовых заданий ЕГЭ
Задание 1.
Дано: прямоугольный параллелепипед с измерениями 3, 4 и 12 см.
Необходимо найти длину одной из главных диагоналей фигуры.
Решение: Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина. На рисунке ниже приведен пример правильного оформления условий задания.
Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:
После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.
Задание 2.
Дано: наклонный параллелепипед с боковым ребром 10 см, прямоугольник KLNM с измерениями 5 и 7 см, являющийся сечением фигуры параллельным указанному ребру.
Необходимо найти площадь боковой поверхности четырехугольной призмы.
Решение: Сначала необходимо зарисовать дано.
Для решения данного задания необходимо применить смекалку. Из рисунка видно, что стороны KL и AD – неравны, как и пара ML и DC. Однако, периметры данных параллелограммов очевидно равны.
Следовательно, боковая площадь фигуры будет равна площади сечения помноженной на ребро AA1, так как по условию ребро перпендикулярно сечению. Ответ: 240 см2.