Определение параметров для модели Hardening Soil. Практика
В статье автор делится практическим опытом подготовки и интерпретации данных инженерно-геологических изысканий для определения характеристик модели Hardening Soil. Затрагиваются спорные вопросы, способы их решения, а также сделана попытка их обоснования на примерах конкретных лабораторных испытаний. Основное внимание уделено назначению граничных условий при проведении трехосных и компрессионных испытаний грунта для определения модулей деформации при 50% прочности, одометрического модуля, модуля разгрузки / повторной нагрузки, степенного показателя Ohde. При определении каждого параметра для подтверждения и доказательства верности выводов, прикреплены результаты лабораторных испытаний с их интерпретацией.
Модель Hardening Soil (модель с двойным упрочнением) заслуженно считается самой распространённой при выполнении геотехнических расчетов в программах конечно-элементного моделирования. Ее популярность по сравнению более простой идеально упругопластической моделью Кулона-Мора объясняется более точным совпадением математического моделирования с опытными данными. Повторение сложного поведения грунта при нагружении достигнуто путем введения гиперболической зависимости (нелинейности) поведения вместо билинейной, учета повышения жесткости с повышением напряжения (с глубиной) по степенному закону, введение модуля деформации по ветви вторичного нагружения, возможности учета коэффициента переуплотнения OCR и так далее. Несмотря на достаточно длительный период использования программ типа Plaxis и модели упрочняющегося грунта, до сих пор встречается некоторое непонимание при определении основополагающих параметров модели.
При проектировании объектов метрополитена в г. Москве большинство расчетов выполняется с помощью программ конечно-элементного анализа и с использованием модели упрочняющегося грунта. Все станционные котлованы, а также глубокие котлованы для притоннельных сооружений проходят экспертизу только при наличии расчетов с использованием модели «Hardening Soil». Более того, на сегодняшний день, уже невозможно согласовать расчеты, не имея прямых лабораторных испытаний для модели «HS».
В данной работе автор останавливается на конкретных аспектах определения входных параметров модели, имеющих расхождения интерпретации в различных грунтовых лабораториях.
В статье затрагиваются спорные вопросы, способы их решения, а также сделана попытка их обоснования на примерах конкретных лабораторных испытаний. Основное внимание уделено назначению граничных условий при проведении трехосных и компрессионных испытаний грунта для определения модулей деформации при 50% прочности, одометрического модуля, модуля разгрузки / повторной нагрузки, степенного показателя Ohde. При определении каждого параметра для подтверждения и доказательства верности выводов, прикреплены результаты лабораторных испытаний с интерпретацией.
Полный текст статьи с формулами, таблицами, списком источников и литературы читайте в формате pdf. ЧИТАТЬ
Еще раз о модели упрочняющегося грунта от ее создателей и пользователей
Геотехническое моделирование является очень важным на всех этапах современного строительства, а также при проведении мониторинга во время эксплуатации зданий и сооружений. Многие современные строительные объекты возводятся на фундаментах глубокого заложения, занимают большую площадь и передают на свои грунтовые основания значительные нагрузки, вовлекая в это очень большие объемы грунтов. Во всех частях системы «основание – фундамент – надземная часть здания/сооружения» формируется сложное напряженно-деформированное состояние (НДС), являющееся пространственно неоднородным и изменяющееся во времени в процессе строительства и эксплуатации. Его количественная оценка на всех этапах является сложной задачей и зависит от ряда факторов, в том числе от физико-механических свойств грунтов основания в условиях естественного залегания, исходного НДС массива и изменчивости модулей деформации по глубине.
Усложняющиеся со временем строительные объекты требуют совершенствования старых и разработки новых моделей (математического отображения) механического поведения грунтов и методов численного моделирования, необходимых для расчетов при геотехническом проектировании. Современные механические модели, применяемые в программных комплексах, позволяют решать эти задачи в трехмерной постановке, определять взаимное влияние зданий/сооружений и их оснований, учитывать неоднородность инженерно-геологических условий и процессы, протекающие во времени. Однако достоверность получаемых при численном моделировании численных результатов сильно зависит от правильности выбора грунтовой модели и определения ее параметров.
Одной из самых универсальных механических моделей, применяемых для описания поведения оснований, сложенных многими видами дисперсных грунтов (особенно для зданий/сооружений с фундаментами глубокого заложения, значительными дополнительными нагрузками и сложными траекториями нагружения), является упругопластическая модель с изотропным упрочнением Hardening Soil Model (HSM), или модель упрочняющегося грунта, которая была разработана в рамках классической теории пластического течения, а не теории упругости.
Первое подробное теоретическое описание этой модели было выполнено в 1999 году в докладе «Модель упрочняющегося грунта: разработка и верификация», сделанном на международном симпозиуме по вычислительной геотехнике ее разработчиками – профессором Веймарского международного исследовательского университета «Баухауз» Т. Шанцем (Германия), профессором Штутгартского университета П.А. Вермеером (Германия) и инженером компании PLAXIS b.v. П.Г. Бонньером (Нидерланды) [10]. Здесь мы приведем краткий обзор материалов этого доклада с пояснениями, взятыми из некоторых других работ [1 – 9].
Главными особенностями модели HS являются (рис. 1):
Рис. 1. Гиперболическая зависимость между девиаторным напряжением q=σ1 – σ3 и относительной осевой деформацией ε1 при первичном нагружении в процессе стандартного испытании грунта на трехосное сжатие в дренированных условиях [10]. Буквенные обозначения: E50 – секущий модуль деформации первичного нагружения при 50%-ной прочности, т.е. при 50% от предельного девиаторного напряжения qf ; Eur – модуль при разгрузке и повторном нагружении; qa – асимптотический уровень прочности, к которому стремится зависимость; qf – предельное девиаторное напряжение, рассчитанное по закону Кулона
Математическая формулировка модели упрочняющегося грунта использует:
Модель упрочняющегося грунта дает возможность моделировать нелинейность деформаций, остаточные перемещения при разгрузке и отражает переуплотнение грунтов основания с помощью коэффициента переуплотнения OCR.
HSM позволяет более достоверно описывать поведение грунтовых оснований, чем модель Мора – Кулона (последняя хорошо подходит только для описания допредельных состояний грунта, поскольку не учитывает изменения модуля деформации при изменении уровня напряжений в массиве, а также при разгрузке и повторном нагружении грунта и занижает значения дополнительных осадок фундамента).
В отличие от идеально-упругопластической модели с критерием прочности Мора – Кулона, положение поверхности текучести (границы области допустимых напряжений для сохранения упругого поведения) в модели упрочняющегося грунта не является фиксированным в пространстве главных напряжений. Ограниченное ею пространство упругого поведения может расширяться вследствие пластического деформирования. При этом модель подразумевает различие между двумя основными видами упрочнения – при сдвиге и при сжатии. Она учитывает в том числе зависимость модуля жесткости (деформации) от напряжений, поэтому все параметры жесткости в ней увеличиваются с ростом давления.
Модель упрочняющегося грунта достаточно хорошо описывает развитие сдвиговых деформаций при девиаторном нагружении и объемных деформаций при всестороннем обжатии. Она достаточно точно отражает поведение грунта при экскавации, устройстве подпорных стен и проходке туннелей, когда происходит уменьшение среднего эффективного напряжения и одновременно мобилизация сопротивления пород сдвигу. Ограничения этой модели заключаются в том, что она не очень подходит для расчетов оснований, сложенных слабыми сильносжимаемыми грунтами, непригодна для моделирования динамических процессов и не может учесть анизотропию прочности и жесткости, а также ползучести и длительной прочности. Следует также отметить, что HSM не учитывает разупрочнение грунта в результате эффектов дилатансии ( изменений объема, наблюдаемых в дисперсных материалах, когда они подвергаются сдвиговым деформациям ). Поэтому для высокоточного моделирования циклического нагружения требуются более сложные модели.
HSM использует три модуля деформации:
Суммарные деформации в HSM рассчитываются с использованием зависимой от нагрузки жесткости, различной для первичного нагружения и для разгрузки и повторного нагружения. Эти пластические деформации вычисляются путем введения мультиповерхностного критерия пластичности (текучести). Принимается, что упрочнение является изотропным в зависимости как от пластического сдвига, так и от объемной деформации. Закон пластического течения принимается неассоциированным для фрикционного упрочнения при сдвиговом деформировании и ассоциированным для упрочнения на шатровой поверхности текучести в модифицированной модели Друкера – Прагера (кэп-модели – cap-model) – не зависящей от скорости нагружения упругопластической модели, которая предполагает материал однородным и изотропным.
Поверхности текучести в ходе сдвигового упрочнения показаны на рисунке 2. Кривые текучести по мере деформирования поднимаются до предельной кривой Мора – Кулона. Их форма зависит от показателя степени m в формуле, отражающей зависимость жесткости (модуля деформации E50 ) от напряжения (формула (3) в табл. 1). При m =1 линии получаются прямыми, а при m – слегка изогнутыми.
Рис. 2. Поверхности текучести в ходе сдвигового упрочнения твердого грунта при показателе степени m в зависимости жесткости от напряжения, равном 0,5. Значения параметра упрочнения (пластической деформации сдвига γ p ) возрастают для кривых снизу-вверх. При построении таких кривых текучести нужно использовать уравнения (3), (4), (7), (8) из табл. 1 [10]
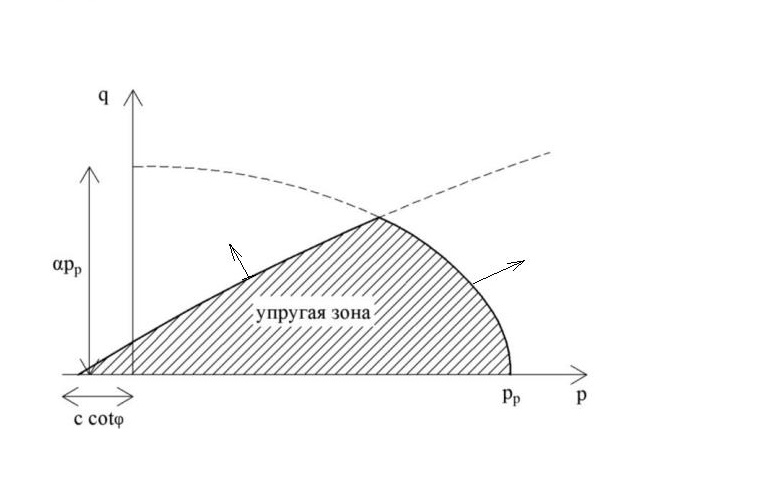
Рис. 3. Упругая зона, ограниченная поверхностью текучести при сдвиге (линия над заштрихованной областью) и поверхностью текучести при сжатии с соответствующей объемной пластической деформацией (эллиптическая линия справа от заштрихованной зоны). Стрелками показаны направления смещения поверхностей текучести при сдвиговом (сверху) и объемном (справа) упрочнении [1, 10]
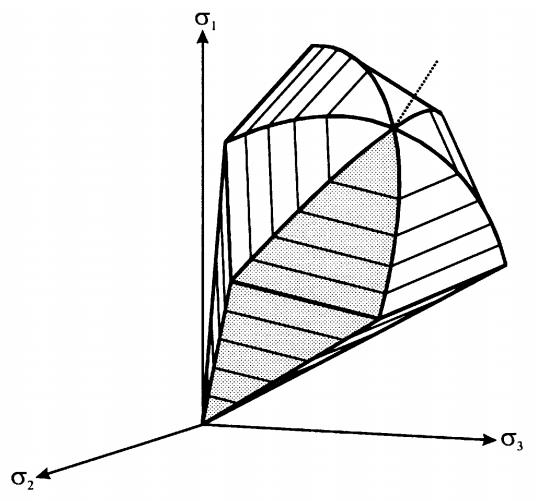
Рис. 4. Трехмерное представление суммарной поверхности текучести для модели упрочняющегося грунта в пространстве главных напряжений для несвязного грунта [10]
Модель упрочняющегося грунта записывается в виде ряда математических выражений – прежде всего основных уравнений для модулей жесткости, пластического течения (текучести), разрушения и поверхностей текучести, которые совпадают с поверхностями потенциала пластической деформации для устойчиво пластического материала (табл. 1, 2).
Модель HS можно использовать для расчетов в том числе в программном комплексе PLAXIS на основе метода конечных элементов (МКЭ).
Численное моделирование с использованием HSM по сравнению с моделью Мора – Кулона требует больше входных параметров, для определения которых помимо стандартных компрессионных испытаний необходимо выполнить трехосные испытания в консолидировано-дренированных условиях с использованием стабилометров. Об определении параметров для численного моделирования поведения дисперсных грунтов с использованием модели упрочняющегося грунта хорошо рассказано в статье [5].
Для использования этой модели необходимо задать следующие основные параметры :
1) параметры прочности:
2) параметры жесткости:
3) дополнительные параметры:
Остальные параметры можно принять по рекомендациям разработчиков [8, 10].
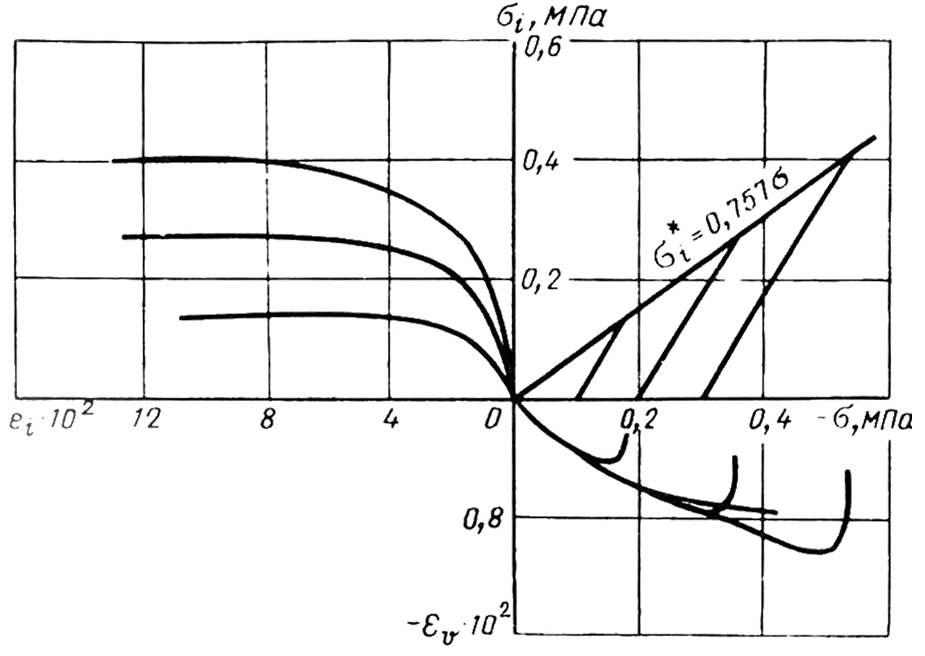
Модель упрочняющегося грунта была откалибрована ее разработчиками [10] путем обратного расчета результатов трехосных и одометрических испытаний рыхлого «хостунского» песка (с начальным коэффициентом пористости e0 =0,89), параметры которого хорошо известны и для которого имеется много доступных экспериментальных данных, поскольку он часто используется в геотехнических исследованиях. С помощью HSM и компьютерной программы Plaxis на основе МКЭ были получены численные модели испытаний на недренированный сдвиг и прессиометрических испытаний в калибровочной камере. Для обеих проверок модели экспериментальные и численные результаты оказались довольно близкими друг к другу, что авторы работы [10] сочли очень перспективным.
С помощью такой откалиброванной модели удобно выполнять обратные расчеты результатов испытаний на недренированный сдвиг и прессиометрических тестов.
Предложенная в работе [10] модель упрочняющегося грунта оказалась весьма привлекательной для использования в повседневной геотехнической практике. С точки зрения ее авторов, дальнейшие разработки должны были бы включать расширение базы данных в поле параметров жесткости для связных грунтов, применение предложенной модели для решения краевых задач (нахождения предельных значений), в которых актуальна жесткость при малых деформациях, а также трехмерную верификацию модели. И эти разработки с момента предложения HSM активно проводятся разными авторами во всем мире.
Список литературы и других источников
Кстати, для желающих больше узнать о работе модели HS и других моделей, проводится множество курсов повышения квалификации. Мы рекомендуем курсы в геотехнической лаборатории АО «МОСТДОРГЕОТРЕСТ». Подробнее о них можно узнать на официальном сайте организации www.mdgt.ru
Заглавное фото предоставлено АО «МОСТДОРГЕОТРЕСТ».
Выбор модели грунта и её параметров в расчётах геотехнических объектов
А. И. Голубев
ГОУ ВПО СПбГПУ, Санкт-Петербург, Россия
А. В. Селецкий
ООО «НИП-Информатика», Санкт-Петербург, Россия
АННОТАЦИЯ: Статья посвящена вопросу обоснования выбора математической модели грунта и определению ее параметров. В качестве сопоставляемых моделей выбраны две наиболее популярные упругопластические модели: модель Кулона-Мора и модель упрочняющегося грунта. Приведены результаты методики определения расчетных параметров этих моделей путем сопоставления результатов компьютерного моделирования стабилометрических испытаний в программе PLAXIS с лабораторными данными. В рамках выбранных моделей выполнены расчеты напряженно-деформированного состояния грунтовых массивов с ограждающими конструкциями. Дан анализ выявленных характерных различий в прогнозе деформаций объектов и усилий в конструкционных элементах.
1. Введение
Комплексное расчетное обоснование проектов строительства, эксплуатации, реконструкции сооружений в сложных инженерно-геологических условиях, в том числе в стесненной городской застройке, стало невозможным без использования современных компьютерных программ. При этом следует помнить, что расчеты, по результатам которых будет принято проектное решение, следует проводить только после серии предварительных расчетов исследовательского характера, учитывающих влияние ряда факторов при математическом моделировании работы геотехнической системы. Наиболее важными из них являются вопросы создания геометрической модели, конечно-элементной расчетной схемы и выбора модели грунта.
В современной практике геотехнических расчетов используются математические модели грунта разной степени сложности. Преимущество простых моделей заключается в меньшем количестве входных параметров, а также в простоте и ясности определяющих уравнений. Однако результаты моделирования в этом случае могут быть достаточно грубыми и плохо согласующимися с реальными данными. Сложные, усовершенствованные модели позволяют
описать поведение грунта более точно, но они требуют более широкого набора характеристик грунта, а также достаточной осведомленности и опытности инженера при выборе модели, ее параметров и анализе полученных результатов расчетов.
2. Две альтернативные модели
Декларируемый в строительных нормах принцип проектирования по предельным допускаемым деформациям может быть реализован в полной мере только при использовании упругопластических моделей грунта, позволяющих описывать напряженно-деформированное состояние на всем диапазоне изменения нагрузок, вплоть до предельных (разрушающих) значений. Возьмем две такие модели: упругоидеальнопластическую модель (модель Кулона-Мора) (Бугров, 1974) и упругопластическую модель с упрочнением (Schanz et al, 1999). Эти модели включены в программный комплекс PLAXIS, что позволяет провести сравнительный анализ и оценить влияние выбранной модели и ее расчетных параметров на прогнозируемое развитие напряженно-деформированного состояния грунта.
3. Определение параметров моделей. Лабораторные и виртуальные испытания грунта
Программа PLAXIS располагает опцией оперативного математического моделирования стандартных лабораторных испытаний грунтов с использованием имеющихся расчетных моделей (опция «soil test»).
Таблица 1. Расчетные параметры моделей грунта
Обзор статьи
Главное меню
Сравнение результатов численных расчетов с использованием современных моделей грунта (Hardening Soil, Hardening Soil Small и Generalized Hardening Soil) с результатами мониторинга
Страницы:
Аннотация:
Список цитируемой литературы:
Likitlersuang S., Surarak C., Wanatowski D., Oh E., Balasubramaniam A. Finite element analysis of a deep excavation: A case study from the Bangkok MRT // Soils and Foundations. 2013. Vol. 53 (5). Pp. 756-773. DOI: 10.1016/J.SANDF.2013.08.013
Law K. H., Othman S. Z., Hashim R., Ismail Z. Determination of soil stiffness parameters at a deep excavation construction site in Kenny Hill Formation // Measurement. 2014. Vol. 47. Pp. 645-650. DOI: 10.1016/J.MEASUREMENT.2013.09.030
Brinkgreve R. B. J., Kumarswamy S., Swolfs W. M. PLAXIS CONNECT Edition V20. Material Models Manual. URL: https://communities.bentley.com/cfs-file/__key/communityserver-wikis-com. (дата обращения: 22/02.2021)
Hardin B. O., Black W. L. Closure on vibration modulus of normally consolidated clay // Proc. ASCE: Journal of the Soil Mechanics and Foundations Division. 1969. Vol. 95. No. SM6. Pp. 1531-1537
Laera A., Brinkgreve R. B. J. (eds.). PLAXIS. Site response analysis and liquefaction evaluation. 2015. Pp. 1-42
Мангушев Р. А., Дьяконов И. П., Кондратьева Л. Н. Границы практического применения свай «Фундекс» в условиях слабых грунтов // Жилищное строительство. 2017. № 9. С. 3-8
Дьяконов И. П., Конюшков В. В. Особенности работы набивной завинчиваемой сваи «Фундекс» в разнородных грунтах // Вестник гражданских инженеров. 2014. № 6 (47). С. 116-120
Мангушев Р. А., Ершов А. В., Осокин А. И. Современные свайные технологии. М.: АСВ, 2010. 235 с
Разработан и введен в действие новый СТО
Сотрудниками лаборатории освоения подземного пространства городов и лаборатории механики грунтов НИИОСП им. Н.М. Герсеванова разработан и введен в действие с 01.09.2021г. СТО 36554501-067-2021 «Лабораторное определение параметров моделей нелинейного механического поведения грунтов с объемным и двойным упрочнением».
Настоящий стандарт организации устанавливает требования к лабораторным методам определения параметров геотехнических моделей нелинейного механического поведения грунтов с объемным и двойным упрочнением, применяемых для геотехнических расчетов дисперсных грунтов с использованием геотехнических программных комплексов.
Стандарт распространяется на определение параметров моделей Soft Soil, Soft Soil Creep, Hardening Soil, Hardening soil with small strain, реализованных в геотехническом программном комплексе PLAXIS. Применение стандарта для определения параметров моделей, реализованных в других геотехнических программных комплексах допустимо при использовании аналогичных моделей механического поведения грунта.
Действие стандарта не распространяется на определение параметров моделей многолетнемерзлых, просадочных, набухающих, засоленных, органоминеральных и органических, эллювиальных, намывных, насыпных (II и III типа), пучинистых, закрепленных и скальных грунтов.


+7 (495) 602-00-70, (499) 170-15-48, г. Москва, 2-я Институтская ул., д.6.
© Copyright 2013-2021 НИЦ Строительство
Все права защищены