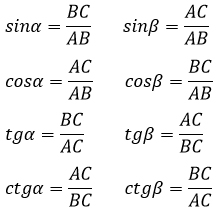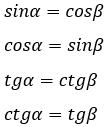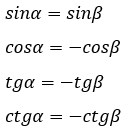Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
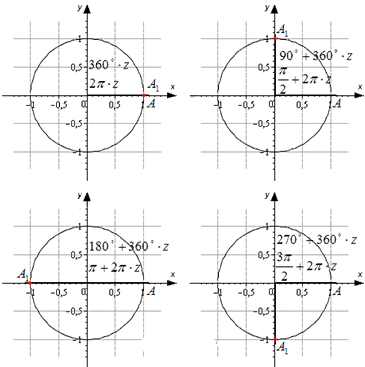
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
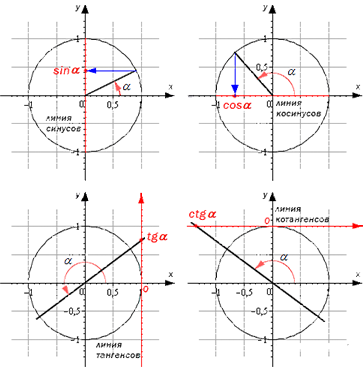
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
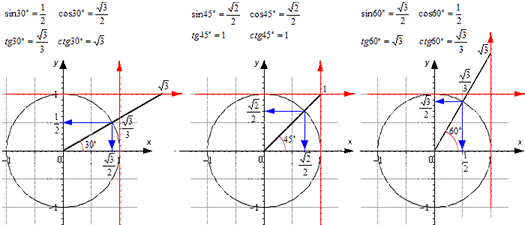
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
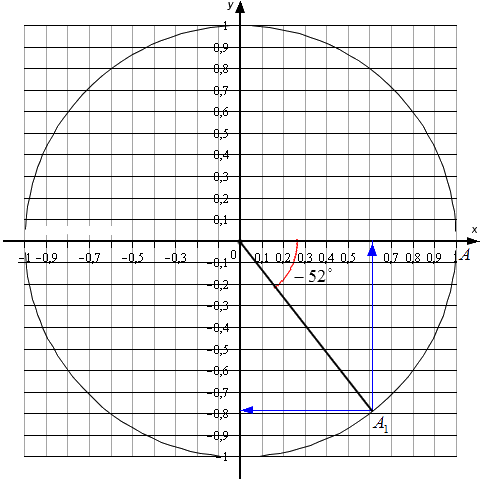
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Сведение к углу
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Синус, косинус, тангенс и котангенс
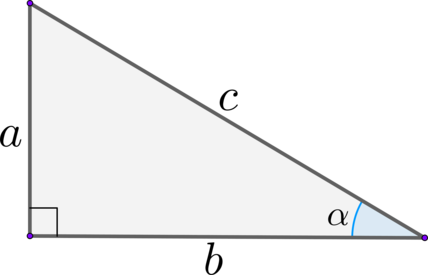
Острые углы в прямоугольном треугольнике.
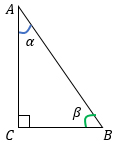
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
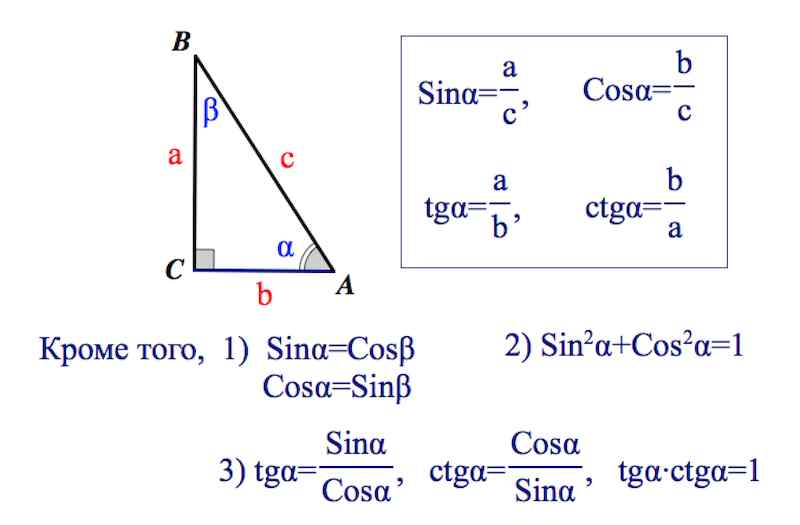
Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Смежные углы.
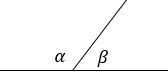
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для «прекрасных» углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgα | 0 | √3/3 | 1 | √3 | — | 0 | — | 0 |
| ctgα | — | √3 | 1 | √3/3 | 0 | — | 0 | — |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Начальные сведения о синусе, косинусе, тангенсе и котангенсе
Определения
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm
Утверждение
Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.
Теорема
Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:
Утверждение
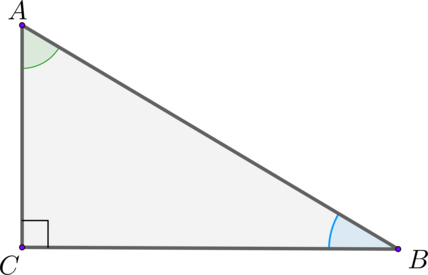
В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\) :
\(\sin \angle A=\cos \angle B\)
Доказательство
Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.
Теорема
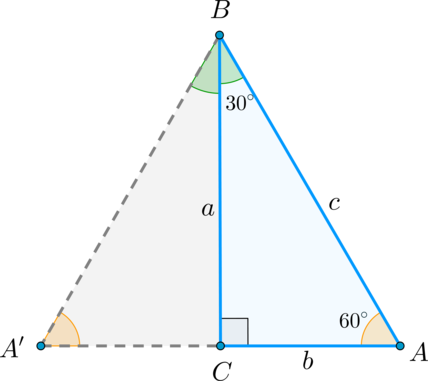
Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:
\[<\large<\begin
Доказательство
Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac<\sqrt3>2\)
Замечание
Для простоты запоминания таблицы можно записать ее в следующем виде:
Теорема
Справедливы следующие формулы приведения:
\[\begin
Пример
Учащиеся, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение конкурентных баллов по итогам его прохождения, непременно должны повторить теорию о синусе, косинусе, тангенсе и котангенсе. Как показывает практика, задания по данной тематике ежегодно встречаются в аттестационном испытании. Таким образом, если одним из ваших слабых мест являются формулы и теоремы синусов, косинусов, тангенсов и котангенсов, рекомендуем освежить в памяти базовую теорию. В этом вам поможет образовательный портал «Школково». В соответствующем разделе представлена теория о синусах, косинусах, тангенсах и котангенсах, которая позволит вам подготовиться к сдаче экзамена. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Ознакомившись с теорией, выпускник сможет грамотно объяснять решение задач ЕГЭ на синусы, косинусы, тангенсы и котангенсы. В этом состоит половина успеха при прохождении аттестационного испытания.
Для того чтобы учащиеся из Москвы или другого населенного пункта России, посетившие наш ресурс, смогли легко и качественно подготовиться к ЕГЭ, мы не только в понятной форме изложили теорию косинусов, синусов, тангенсов и котангенсов, но и подобрали соответствующие упражнения. Для каждого из них наши специалисты прописали подробный алгоритм решения и правильный ответ. Выполняя такие задачи при подготовке к ЕГЭ по математике, выпускники смогут лучше закрепить изученную теорию синусов и косинусов в треугольнике. Выбрать простые и более сложные упражнения вы можете в разделе «Каталог».
Изучив теорию о синусах, косинусах, тангенсах и котангенсах и попрактиковавшись в решении задач по данной теме при подготовке к ЕГЭ, учащиеся имеют возможность сохранить любое задание в «Избранное», чтобы при необходимости обсудить его с преподавателем.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
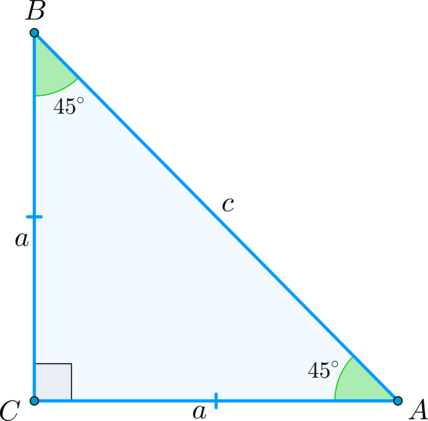
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Синус, косинус, тангенс в прямоугольном треугольнике

Подробнее про прямоугольный треугольник здесь.
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
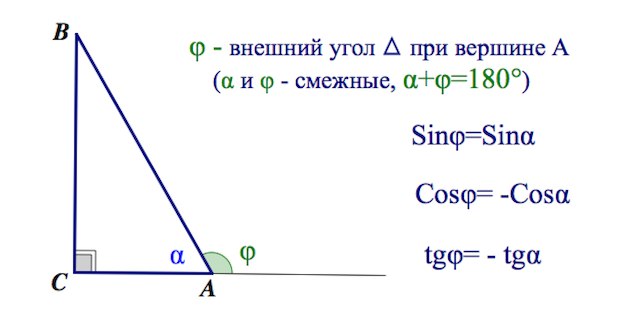
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Чтобы не потерять страничку, вы можете сохранить ее у себя: